


for eg., order 4 has 880 possible magic squares, 05224 and 6 has approximately 1.7745×10^19. Now, the number of possible magic squares increases dramatically with order. The downside is that your program will only generate a limited number of magic squares, i.e, only those that can be generated using the known algorithms for odd, even and doubly-even orders. What you've done is a good example of coding a well-known algorithm. What's wrong with my Magic Square program? Int i= 0, j=n/2 // start position for ( int k= 1 k > &matrix, int n) Void OddMagicSquare(vector > &matrix, int n)
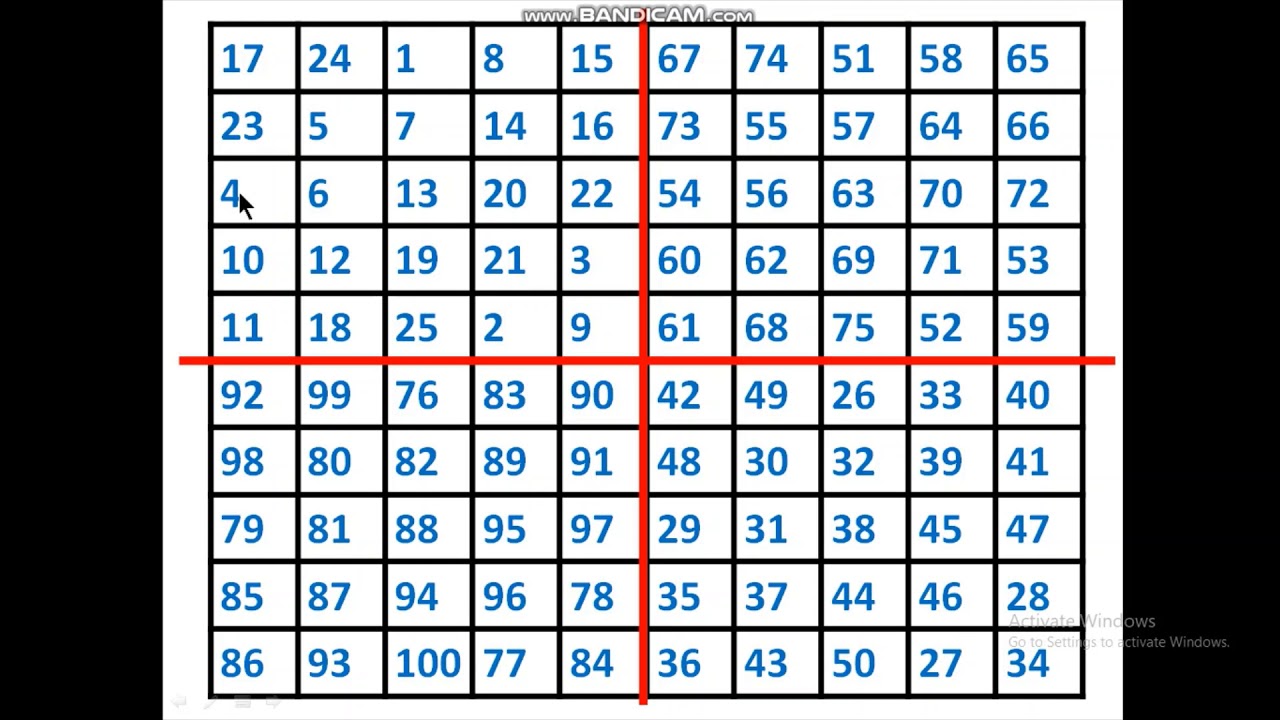
Void PrintMagicSquare(vector > &matrix, int n) Įlse // n is even if (n%4= 0) // doubly even order Void MagicSquare(vector > &matrix, int n) Void SinglyEvenMagicSquare(vector > &matrix, int n) Void DoublyEvenMagicSquare(vector > &matrix, int n)


 0 kommentar(er)
0 kommentar(er)
